Güte des Fit -

Güte des Fit - $\ensuremath{\chi^2}$

Der Wert des $\ensuremath{\displaystyle \ensuremath{\chi^2}}$ Fits am Minimum liefert auch gleichzeitig ein Mass für die Güte des Fits. Wenn die Unterschiede zwischen den gemessenen ( $\ensuremath{\displaystyle y_i}$ ) und gefitteten ( $\ensuremath{\displaystyle f(x_i,\vec{a}}$ ) Werten konsistent mit statistischen Schwankungen sind erwartet man ein $\ensuremath{\displaystyle \ensuremath{\chi^2}}$ gemäss der $\ensuremath{\displaystyle \ensuremath{\chi^2}}$ Funktion:

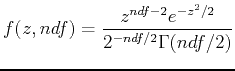
$\ensuremath{\displaystyle f(z, ndf) = \frac{z^{ndf-2} e^{-z^2/2}}{2^{-ndf/2} \Gamma(ndf/2)} }$

wobei $\ensuremath{\displaystyle ndf}$ die Zahl der Freiheitsgrade ist, $\ensuremath{\displaystyle ndf = N_{points} - N_{par}}$ .

Bei vielen Wiederholungen des Experiments bzw. Fits sollte das resultierende $\ensuremath{\displaystyle \ensuremath{\chi^2}}$ einer solchen Verteilung folgen.

$\includegraphics[width=.7\textwidth]{chi2_dist2.eps}$

Als Faustregel kann man sich merken:

$\ensuremath{\displaystyle \ensuremath{\chi^2}/ ndf \approx 1}$

Deutlich grössere Werte sind ein klarer Hinweis auf konzeptionelle Probleme, entweder sind die Fehler unterschätzt oder die angepasste Funktion ist nicht geeignet zur Beschreibung der Daten. Kleine Werte deuten auf zu große Fehler hin, typisch sind falsch bestimmte statistische Fehler.

In ROOT:

Funktion TMath::Prob(double chi2, int ndf )
Liefert Wahrscheinlichkeit $\ensuremath{\displaystyle \ensuremath{\chi^2}>= chi2 }$ bei Freiheitsgraden zu bekommen, z.B.:
TMath::Prob( 1.0, 3) = 0.801
TMath::Prob( 3.0, 3) = 0.392
TMath::Prob( 8.5, 3) = 0.037

GDuckeck 2018-04-10