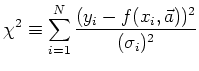
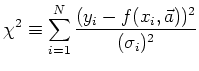
Dann muss die `Kovarianzmatrix' für den Fit benutzt
werden.
Für
![]() Werte
Werte
![]() beschreibt die
beschreibt die
![]() Kovarianzmatrix
Kovarianzmatrix
![]() Fehler und Korrelationen der einzelnen Werte:
Fehler und Korrelationen der einzelnen Werte:
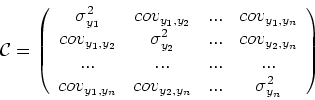
mit
![]() .
.
Das
![]() wird dann gemäss der allgemeinen Formel
wird dann gemäss der allgemeinen Formel
Zum Erstellen und Invertieren der Kovarianzmatrix
![]() empfiehlt sich die ROOT Klasse TMatrixD.
empfiehlt sich die ROOT Klasse TMatrixD.
![]() Resonanzkurve des Wirkungsquerschnitts
Resonanzkurve des Wirkungsquerschnitts
Gutes Beispiel für korrelierte Fehler ist Messung des Wirkungsquerschnitts bei LEP im Bereich der
![]() Resonanz.
Resonanz.

![$\textstyle \parbox{.45\textwidth}{
\begin{center}
\mbox{
\includegraphics[width=.45\textwidth]{ls.eps}}
\end{center}
}$](img48.png)
Klassische Messung, auch im Fortgeschrittenen Praktikum an der LMU !
![$\textstyle \parbox{10.1cm}{
\includegraphics[height=5cm,bb=19 24 566 572]{ee.eps}
\includegraphics[height=5cm,bb=19 24 566 572]{mm.eps}
}$](img50.png)
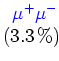
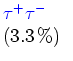
![$\textstyle \parbox{10.1cm}{
\includegraphics[height=5cm,bb=19 24 566 572]{tt.eps}
\includegraphics[height=5cm,bb=19 24 566 572]{mh.eps}
}$](img53.png)
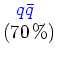
Entsprechender Fit mit Minuit:
#include "TMatrix.h"
TMatrixD *cov;
double *val;
double *xval;
const int nv = 7;
void setInput()
{ // define input
val = new double[nv];
xval = new double[nv];
cov = new TMatrixD(nv,nv);
double xv[nv] = { 88.396, 89.376, 90.234, 91.238, 92.068, 93.080, 93.912 };
double yv[nv] = { 6.943, 13.183, 25.724, 40.724, 27.031, 12.273, 6.980 };
double ey[nv] = { 0.087, 0.119, 0.178, 0.087, 0.159, 0.095, 0.064};
double rsys = 0.004; // correllated relative syst uncertainty on yv
for ( int i=0; i<nv; i++ ) {
val[i] = yv[i];
xval[i] = xv[i];
cov(i,i) = ey[i]*ey[i]; // stat errors
for ( int j=i; j<nv; j++ ) {
cov(i,j) = cov(i,j) + yv[i] * yv[j] * rsys * rsys;
cov(j,i) = cov(i,j);
}
}
cov->Print();
cov->Invert();
cov->Print();
}
double BreitWig( double *x, double *par)
{
// Breit- Wigner function
double mw = par[0], gw = par[1], spk=par[2], mw2, gw2, eb2;
mw2 = mw*mw;
gw2 = gw*gw;
eb2 = x[0]*x[0];
return( spk * gw2*mw2 / ( pow( eb2 - mw2, 2 ) + mw2 * gw2 ) );
// return( spk * gw2*mw2 / ( pow( eb2 - mw2, 2 ) + eb2*eb2/mw2 * gw2 ) );
}
void fcn(Int_t &npar,double *gin, double &f, double *par, int iflag)
{
// calculate Chi2
double chi2 = 0.;
for ( int i=0; i<nv; i++ ) {
double fvali = BreitWig( &xval[i], par );
for ( int j=0; j<nv; j++ ) {
double fvalj = BreitWig( &xval[j], par );
chi2 += ( fvali - val[i] ) * cov(i,j) * ( fvalj - val[j] ) ;
}
}
// cout << "Chi2 = " << chi2 << endl;
f = chi2;
}
void bwfitmnc()
{
setInput();
// initialize TMinuit
const int npar = 3;
gMinuit = new TMinuit(npar);
// Tell Minuit the function
gMinuit->SetFCN(fcn);
// Start Werte fuer Minuit
int ierflg;
gMinuit->mnparm(0, "mass", 85, 0.1, 0., 0., ierflg);
gMinuit->mnparm(1, "width", 2., 0.1, 0., 0., ierflg);
gMinuit->mnparm(2, "speak", 10., 0.1, 0., 0., ierflg);
// minimization
double arglist[3] = { 1000., 1., 0. };
gMinuit->mnexcm("MIGRAD", arglist ,1,ierflg);
// fcn( nparfit, &zero, &chi2, par, 5, 0 );
// TGraphErrors *tg = new TGraphErrors( 7, xv, yv, ex, ey );
//tg->Draw("AP");
// central value
double par[npar], epar[npar];
for ( int i=0; i<npar; i++ ) {
gMinuit->GetParameter( i, par[i], epar[i] ) ;
}
double ey[nv] = { 0.087, 0.119, 0.178, 0.087, 0.159, 0.095, 0.064};
for ( int i=0; i<nv; i++ ) {
// double delta = (yv[i] - f->Eval(xv[i]);
double delta = (val[i] - BreitWig(&xval[i], par));
cout << val[i] << " +- " << ey[i] << " delta: " << delta << " " << delta/ey[i] << endl;
}
}
Berücksichtigung von Fehlern in der x-Koordinate
Bei Messungen von
![]() Wertepaaren gibt es oft Fehler nicht nur in
Wertepaaren gibt es oft Fehler nicht nur in
![]() sondern auch in
sondern auch in
![]() .
.
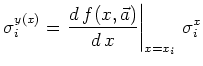
#include "TMatrix.h"
TMatrixD *cov;
double *val;
double *xval;
const int nv = 7;
void setInput( bool deltax = true, double * par = 0 )
{ // define input
val = new double[nv];
xval = new double[nv];
cov = new TMatrixD(nv,nv);
double xv[nv] = { 88.396, 89.376, 90.234, 91.238, 92.068, 93.080, 93.912 };
double yv[nv] = { 6.943, 13.183, 25.724, 40.724, 27.031, 12.273, 6.980 };
double ey[nv] = { 0.087, 0.119, 0.178, 0.087, 0.159, 0.095, 0.064};
double rsys = 0.004; // correlated relative syst uncertainty on yv
double esys = 0.007; // 7 GeV syst error on x=E (absolute)
TF1 * f1;
if ( deltax ) {
// use as Root function
TF1 * f1 = new TF1( "bw", BreitWig, 70, 100, 3 );
f1->SetParameters( par );
}
for ( int i=0; i<nv; i++ ) {
val[i] = yv[i];
xval[i] = xv[i];
(*cov)(i,i) = ey[i]*ey[i]; // stat errors
for ( int j=i; j<nv; j++ ) {
(*cov)(i,j) = (*cov)(i,j) + yv[i] * yv[j] * rsys * rsys;
if ( deltax ) { // treat errors in x, use TF1 Derivative method
double dydxi = f1->Derivative( xv[i] ); // slope at x[i]
double dydxj = f1->Derivative( xv[j] ); // slope at x[j]
(*cov)(i,j) = (*cov)(i,j) + dydxi * esys * dydxj * esys;
}
(*cov)(j,i) = (*cov)(i,j);
}
}
cov->Print();
cov->Invert();
cov->Print();
}
...
void bwfitmnce()
{
setInput(false);
// initialize TMinuit
const int npar = 3;
gMinuit = new TMinuit(npar);
// Tell Minuit the function
gMinuit->SetFCN(fcn);
// Start Werte fuer Minuit
int ierflg;
gMinuit->mnparm(0, "mass", 85, 0.1, 0., 0., ierflg);
gMinuit->mnparm(1, "width", 2., 0.1, 0., 0., ierflg);
gMinuit->mnparm(2, "speak", 10., 0.1, 0., 0., ierflg);
// minimization
double arglist[3] = { 1000., 1., 0. };
gMinuit->mnexcm("MIGRAD", arglist ,1,ierflg);
double par[npar], epar[npar];
for ( int i=0; i<npar; i++ ) {
gMinuit->GetParameter( i, par[i], epar[i] ) ;
}
// include x errors and iterate fit
setInput(true, par);
gMinuit->mnexcm("MIGRAD", arglist ,1,ierflg);
// accurate error matrix
gMinuit->mnexcm("HESSE", arglist ,1,ierflg);
...
}