Next: Fits (II) Up: Übungsaufgaben Previous: Mittelwerte
// 1. Datensatz
{
Float_t xarr[16] = { 0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5,
10.5, 11.5, 12.5, 13.5, 14.5, 15.5};
Float_t yarr[16] = {0.731596, 3.11894, 0.368688, 5.24658, 4.34652,
7.10241, 9.99553, 9.5674, 11.0389, 13.5178, 11.9335,
14.9933, 15.1822, 18.3361, 17.5097, 21.8429};
Float_t exarr[16] = { 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1,
0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1 };
Float_t eyarr[16] = { 0.701041, 0.668213, 1.24997, 1.77685, 0.804879,
1.48788, 0.945508, 0.508232, 0.817365, 1.5927,
1.34098, 1.3508, 0.914614, 1.897, 1.66663, 1.42966};
TGraphErrors *tg = new TGraphErrors( 16, xarr, yarr, exarr, eyarr );
tg->Draw("AP");}
// 2. Datensatz
{
Float_t xarr[16] = { -3.5, -2.5, -1.5, -0.5, 0.5, 1.5,
2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5, 10.5, 11.5};
Float_t yarr[16] = {219., 155., 89., 11.,
54., 80., 48., 5., -47.,
-64., -101., -125., -124., 13.,
239., 525. };
Float_t exarr[16] = { 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1,
0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1 };
Float_t eyarr[16] = { 65., 41, 30., 26., 26., 24.,
18., 4., 17., 33., 45.,
49., 38., 6., 74., 160.};
TGraphErrors *tg = new TGraphErrors( 16, xarr, yarr, exarr, eyarr );
tg->Draw("AP");}
Sie kalibrieren einen Detektor mit Strahlen bekannter Energie
von
![]() und erhalten jeweils
und erhalten jeweils
![]() .
.
Anschliessend messen Sie für ein Teilchen eine Energie
![]() .
.
Was ist die wahre Energie und ihre Unsicherheit,
![]() ?
?
void linefit()
{
float xv[3] = { 60., 80, 100. };
float yv[3] = { 59.73, 80.64, 100.51 };
float ey[3] = { 0.35, 0.38, 0.42 };
float ex[3] = { 0.01, 0.01, 0.01 };
TGraphErrors *tg = new TGraphErrors( 3, xv, yv, ex, ey );
tg->Draw("AP");
}
Machen Sie einen Geradenfit:
![]() .
.
Durch umkehren
![]() bestimmen Sie die wahre Energie, für
bestimmen Sie die wahre Energie, für
![]() müssen
Sie die Fehlerfortpflanzung bemühen, d.h. Sie
brauchen die Kovarianzmatrix für
müssen
Sie die Fehlerfortpflanzung bemühen, d.h. Sie
brauchen die Kovarianzmatrix für
![]() und
und
![]() .
.
(Fitoption "v" oder verbose im Fit-panel)
void tfbw()
{
Double_t ecm = 200, mw = 80;
Double_t gamma_w = 2; // W Zerfallsbreite
Double_t eb, beta, gamma;
Double_t xrnd;
// initialize
eb = ecm/2.; // beam energy
// define Breit-Wigner function
TF1 *fbw = new TF1("fbw", BreitWig, 70, 90, 3);
// set the parameters
fbw->SetParameters( mw, gamma_w,1.);
TH1F * hbw = new TH1F("hbw", "Breit Wigner", 100, 70, 90);
for ( Int_t i = 0; i < 1000; i++ ) hbw->Fill(fbw->GetRandom());
}
Double_t BreitWig( Double_t *x, Double_t *par)
{
// Breit- Wigner function
Double_t mw = par[0], gw = par[1], mw2, gw2, eb2;
mw2 = mw*mw;
gw2 = gw*gw;
eb2 = x[0]*x[0];
return( par[2]*gw2*mw2 / ( pow( eb2 - mw2, 2 ) + mw2 * gw2 ) );
}
Versuchen Sie zunächst das Histogramm mit einer Gauss-Verteilung zu fitten. Variieren Sie dabei den Fit-range bis die Verteilung annähernd durch einen Gauss-Fit beschrieben wird.
Anschliessend fitten Sie direkt die Breit-Wigner Funktion:
| ROOT > fbw->SetParameters(83, 3, 100); |
| ROOT > hbw->Fit("fbw"); |
Testen Sie ob das Fit Resultat von den Startwerten abhängt.
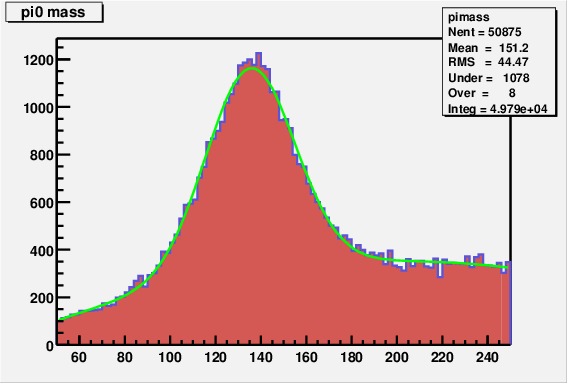
Bestimmen Sie die
![]() Masse und
finden Sie heraus wieviele
Masse und
finden Sie heraus wieviele
![]() im Datensatz enthalten sind
Dazu müssen Sie einen kombinierten Fit machen,
der den Untergrund mit einem Polynom beschreibt und den eigentlichen Signal peak mit einer Gauss Funktion.
im Datensatz enthalten sind
Dazu müssen Sie einen kombinierten Fit machen,
der den Untergrund mit einem Polynom beschreibt und den eigentlichen Signal peak mit einer Gauss Funktion.
TF1("pfit","gaus(0) + pol2(3)", 50, 250)
In diesem Fall müssen Sie Startwerte für die Parameter vorgeben;
fitten Sie zunächst in sub-ranges einen Gauss bzw. Polynom um
vernünftige Anfangswerte zu erhalten.
Anschliessend wird ein
![]() oder Maximum Likelihood Fit durhgeführt.
oder Maximum Likelihood Fit durhgeführt.
Das ganze wird mehrmal (nit) durchgeführt und die jeweils resultierende gefittete Breite in ein Histogramm gefüllt.
Variieren Sie die Zahl der Bins oder der Einträge und vergleichen Sie die Ergebnisse der beiden Fit Methoden, insbesondere wenn nur wenig Einträge pro bin gemacht werden.
gausf2( bool logl = false, int niter = 100, int nrnd = 100, int nbins = 40 )
{
// logl : flag for log-likelihood / chi2 fit
// niter: number of iterations
// nrnd : number of random entries for histo
// nbins: number of bins
double sig;
// create histo
TH1D * h4 = new TH1D("h4","Random Gauss",nbins,-4,4);
// hist for sigma
TH1D * sigma = new TH1D("sigma","sigma from gaus fit",20,0.5,1.5);
for ( i =0; i<niter; i++ ) {
// reset histo contents
h4->Reset();
// fill histo
for ( int j = 0; j<nrnd; j++ ) {
h4->Fill(gRandom->Gaus());
}
if ( logl ) { // likelihood fit
h4->Fit("gaus","lq");
}
else { // Chi2 fit
h4->Fit("gaus","q");
}
// h4->Draw();
// get sigma from fit
TF1 *fit = h4->GetFunction("gaus");
sig = fit->GetParameter(2);
sigma->Fill(sig);
}
sigma->Draw();
}
GDuckeck 2018-04-10